APLICACIÓN DE LA LINGÜÍSTICA MATEMÁTICA A LA GENERACIÓN DE PAISAJES
Dentro del área del tratamiento de imágenes es común encontrar problemas donde se requiere generar paisajes en lo que se incluyan montañas, árboles, nubes, ríos y muchos otros elementos de la naturaleza, por lo que, desde hace algún tiempo y en particular desde el surgimiento de la teoría de Fractales se han desarrollado métodos y técnicas orientados a resolver este problema y específicamente ya se cuenta con una gran cantidad de herramientas que permiten generar montañas, nubes, plantas y otros elementos de un paisaje.
ECUACIÓN FUNDAMENTAL
Las gramáticas surgieron en 1957 a partir de los trabajos de Noam Chomsky y desde principios de los 60’s se han aplicado para representar la estructura de los multiples lenguajes de programación que existen y poder construir los compiladores o intérpretes de estos lenguajes.
En este trabajo se presenta una herramienta basada en la Lingüística Matemática y en particular en una ampliación semántica de las Gramáticas Generativas, con la cual es relativamente fácil representar la estructura de múltiples elementos de la naturaleza, por lo que prácticamnte la misma rutina genera árboles, nubes, montañas, caracoles, estrellas y muchos otros componentes de la naturaleza.
Lo anterior permite desarrollar una herramineta que a partir de la gramática de una familia de imágenes, es capaz de reconocer si una imagen en particular pertenece a la familia o no (como un compilador es capaz de reconocer si una oración pertenece o no a un lenguaje dado). Por otro laso, si se invierte el orden de entradas y salidas se puede tener un sistema capaz de generar imágenes específicas a partir de una gramática dada.
En un principio las producciones encontradas eran diferentes unas de otras pero conforme se siguió atacando el problema se detectó que en muchos casos la regla gramátical encontrada era un caso particular de una regla mas general.
La sorpresa surgió cuando se detecto a su vez todas esas producciones generales eran caso particular de una regla gramáticas mas general aun, que las englobaba a todas.
Encontrándose que prácticamente la estructura gramátical de cualquier elemento de la naturaleza se puede ver como un caso particular de una regla general a la que llamamos Ecuación Fundamental y es de la forma:
S ‡ e*S*
Donde S significa sistema, e es cualquier elemento del sistema (una rama, un tronco, una ladera, etc.), e* significa que se pueden tener tantos elementos como se quieran y S* indica que el sistema puede llamar tantas veces como se quiera. Observe que estamos utilizando el signo * como un factor de repetición, lo cual no es una notación común dentro de las reglas de producción, pero en este caso facilita la rpresentación.
Ejemplo particulares de la ecuación fundamental son:
S ‡ e
S ‡ eS
S ‡ eSS
S ‡ eSS….S
S ‡ eSeeSee….S
ÁRBOLES, ESTRELLAS Y CARACOLESEn particular la ecuación
S ‡ e
Que se lee como el Sistema S llama a e
Representa la estructura de un programa que llama a un elemento, por ejemplo la rutina que gráfica un tronco:
Sistema
{
tronco
}
o mas especificamente
Sistema(x0,y0,long,w)
{
tronco(x0,y0,long,w)
}
donde x0,y0 representan el punto inicial del tronco, long su tamaño y w el ángulo con el que crece.
Como otro ejemplo podemos ver que la ecuación
S ‡ eS
Es equivalente a un sistema que genera un elemento y se llama recursivamente, con lo que, vuelve a generar otro elemento y así sicesivamente.
Sistema
{
elemento
Sistema
}
Esta ecuación engloba por ejemplo a la familia de las estrellas ya que la rutina
Sistema(x0,y0,long,w)
{
elemento(x0,y0,long,w)
Sistema(x0,y0,long,w+w1)
}
Gráfica una recta a partir de un punto (xo,y0)m con un ángulo w y tamaño long y el ángulo se cambia entre llamadas, por lo que al final la rutina genera una estrella.
En el caso de rutinas que dibujab árboles, la estructura iterativa ya no es funcional y en cambio la estructura recursiva es muy simple, por ejemplo la ecuación:
S ‡ eSS
Representa una familia de árboles de 2 ramas y el programa es de la forma
Main()
{
arbol(x0,y0,long,angulo,nivel);
}
arbol(x,y,long,wg,nivel) /*S*/
{
if (nivel > 0) /* condición de terminación */
{
rama(x,y,long,wg,xq,y1); /*e*/
arbol(x1,y1,long/lon1,wg+w1,nivel-1); /*S*/
arbol(x1,y1,long/lon2,wg+w2,nivel-1); /*S*/
}
}
Donde lon1,lon2,w1,w2 son párametros que indican los cambios de tamaño y ángulo de las ramas.
Ahora bien si se requiere dibujar un árbol con tres ramas, simplemente se pondría una llamada recursiva más y así sucesivamente, construir árboles con tres, cuatro, cinco o más ramas se vuelve trivial, ya que su estructura queda:
S ‡ eSSS
S ‡ eSSSS
..
S ‡ eSSS…..S
Y en general la estructura de cualquier árbol es de la forma
S ‡ eS*
UN PROGRAMA GENERALIZADO
Construir un programa para cada tipo de árbol puede llegar a ser tedioso porque al final todos los programas son prácticamente idénticos y es más fácil pensar en un programa general al cual simplemente se le indique cuantas ramas se quieren y se llame a la rutina tantas veces como se necesite.
La ventaja de este enfoque es que el sistema se puede generalizar para representar llamados árboles ‘raros’ como por ejemplo
S ‡ eSe
S ‡ eSSe
S ‡ eeSeSS
S ‡ eSSeeSe
Y cualquier combinación de elementos y llamadas, para lo cual únicamante se necesita preguntar si el comando es una e o una S.
Gramatica[]=’’eSeeSS’’
Main()
{
arbol(x0,y0,l0,w0,nivel)
}
arbol(x,y,long,wg,nivel)
{ si (nivel > 0)
{
I=1
Mientras (gramatica[I] != fin de renglon)
{
si (gramatica[I]=’e’) linea(x,y,l,w,x,x1,y1)
si (gramatica[I]=’S’)
arbol(x1,y1,long/lon[I],wg+wg[I],nivel--)
I++
}
}
}
Si en el arreglo llamado gramática se almacena:
S ‡ e
El sistema genera una línea
S ‡ eS
El sistema genera caracoles o estrellas
S ‡ eSS
El sistema genera árboles con dos ramas
S ‡ eSSS
El sistema genera árboles con tres ramas y así sucesivamente
De donde resulta que el mismo programa que grafica líneas, grafica caracoles y árboles y todos son un caso particular de la estructura
S ‡ e*S*
Por ejemplo si tomamos el siguiente caso particular
Main ()
{
w0=c0; w1=c1; w2=c2; w3=c3; ind=cd;
arbol(x0,y0,1,w0,ind)
{
arbol(x1,y1,1,w,ind)
{
si ind>0
{
linea(x,y,1,w,x1,y1)
arbol(x1,y1,1/1.2,w+w1,ind-1)
arbol(x1,y1,1/1.55,w+w2,ind-1)
arbol(x1,y1,1/1.8,w+w3,ind-1)
}
}
}
donde w0, w1, w2, w3 son el ángulo inicial y los incrementos de ángulos para cada llamada recursiva.
Podemos encontrar que si fijamos w0 =-72, w2=72, w3=144 y modificamos w1 entre 1 y 360 grados, podemos generar una familia completamente diferente, ya que si por ejemplo
w1=24 tenemos un bosque de helechos
w1=4 tenemos una nube en forma de perro
w1=139 tenemos una nube
w1=169 tenemos un fractal de dregón
y así sucesivamente hasta regresar a los helechos.
El anteior efecto se produce si mantenemos fijos w0, w2, w3 y modificamos w1, ahora bien si modificamos cualquiera de los 4 ángulos la cantidad de elementos que se pueden generar es enorme e incluye nubes, árboles y montañas entre otros.
En general las ecuaciones de la forma
S ‡ eSS..S
Permiten generar múltiples familias de árboles, montañas, nubes, rios y prácticamente cualquier elemento de la naturaleza.
Por ejemplo si:
Fijamos w0=-27, w1=6, w2=172 y modificamos w3 se genera una familia de laderas de montaña.
Fijamos w0=-7, w1=6, w2=72 y modificamos w3 se genera una familia de árboles en una ladera y árboles con reflejo.
Fijamos w0=-72, w2=172, w3=144 y modificamos w1 se genera una familia de alacranes.
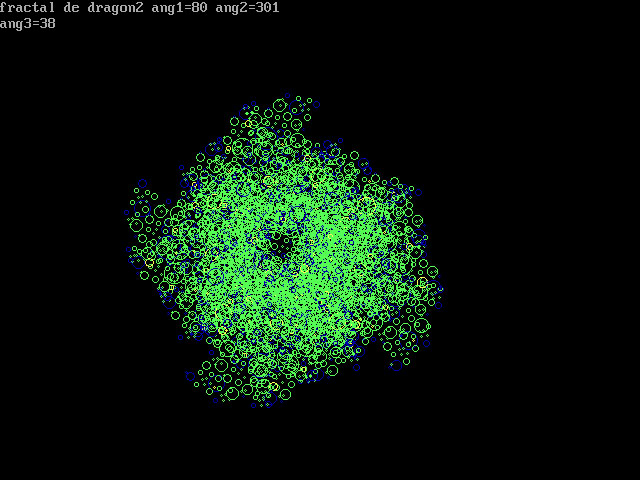

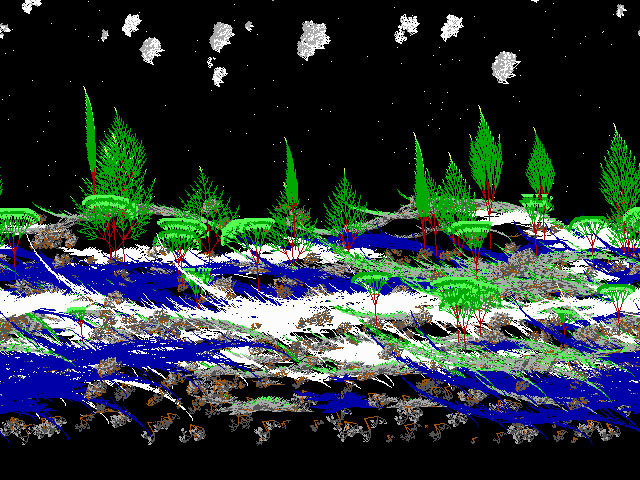
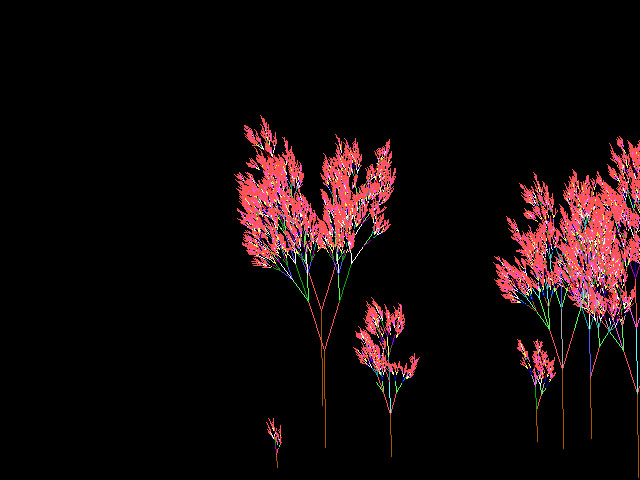
CONCLUSION
En este documento se presento una aplicación de la Lingüistica Matemática a la generación de paisajes, para lo cual: en primer lugar se planteo que existe una ecuación fundamental de la naturaleza de la forma
S ‡ e*S*
Que engloba a las ecuaciones que representan la estructura de troncos, caracoles, estrellas, árboles, nubes y montañas, entre otros. Lo anterior es fundamental ya que nos muestra que multiples fenómenos de la naturaleza tienen la misma estructura.
Este enfoque generaliza y engloba dentro de la lingüistica matemática múltiples herramientas como los métodos iniciador-generador y los de los sistemas-L, con lo que, se puede aprovechar todo el poderío de esta herramienta que se utiliza desde hace muchos años para construir compiladores, reconocer formas, medir la complejidad de sistemas y en general para encontrar y representar la estructura de múltiples problemas de la Informática, por lo que este documento es también una invitación al uso de la Lingüistica Matemática dentro de la graficación y animación.
Como se puede ver estamos llegando a que la estructura de una cantidad enorme de elementos de la naturaleza es la misma, ya que, por ejemplo únicamente cambiando algunos ángulos dentro de una rutina se pueden generar nubes, laderas de montañas, árboles, alacranes, hojas y paisajes en general.
AGRADECIMIENTOS
Muchas gracias a Marina Vicario Solorzano y Francisco Aguilar Vallejo de TECCIZ de México, Cuitlahuac Cantú de ORSA, Sergio Rivera, Francisco Molina C. y Cruz Luna Reyes de UPIICSA-IPN por su ayuda y contribución a este trabajo.
REFERENCIAS
The Synthesys and Rendering of Eroded Fractal terrains.
In Computer Graphics, Vol 23(3), Julio 1989
Developmental Models of Herbaceous Plants for Computer Imagery Purposes.
Computer Graphics, Vol 22(4), Agosto 1988
Generador de Arboles Fractales
En Memorias del III Congreso Nacional sobre Informática y Computación
Jalapa Ver. México, Octubre 1990.
Real Time Design and Animation of Fractal Plants and Trees.
In Computer Graphics, Vol 20)4= SIGGRAPH 86, Agosto 1986
The science of Fractal Images.
De. Springer-Verlag 1988
Sistemas Evolutivos: Nuevo Paradigma de la Informática
En MemoriasXVII conferencia Latinoamericana de Informática, Caracas Venezuela, Julio 1991
Sistemas Evolutivos
En boletin de Política Informática, México, Septiembre 1986
Sintactic Pattern Recognition
De. Addison-Wesley
Aplicaciones de la Lingüistica Matemática y los Fractales a la Generación de Imágenes
En Memorias Simposium Nacional de Computación, México, Noviembre 1991
Teoría Sintáctica
De Anagrama
Formal Languages
De. Academic Press
Las ciencias de lo Artificial
De. ATE
Estructuras Sintácticas
De. Siglo XXI
Formal Languages and Their Relation to Automata
De. Addison-Wesley
©Todos los derechos reservados, se prohibe la reproducción
salvo permiso por escrito del autor.
©All rights reserved, any copying or
duplication of this material is prohibited without written authorization by
its author.
Regresar a Boletines
Regresar a Página Principal del Cpít
ulo
Profesional SIGGRAPH México